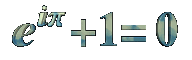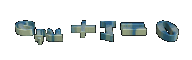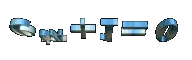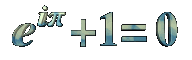Etymologie, Etimología, Étymologie, Etimologia, Etymology, (griech.) etymología, (lat.) etymologia, (esper.) etimologio
@_ Welt, Mundo, Monde, Mondo, World, (lat.) orbis (terrae), (esper.) mondo
Zahlen, Número, Nombre, Numero, Number, (esper.) nombroj, nombroteorio
Zahl 27182 in Alltag und Sprache
A
B
C
D
E
"§"
Eulersche Identität (W3)
Die "Eulersche Identität" e^(i*pi)+1=0 trägt den Namen von "Leonhard Euler" (15. April 1707, Basel (Schweiz) - 18. September 1783, Sankt Petersburg).
(E?)(L?) http://www.math.dartmouth.edu/~euler/index.html
(E?)(L?) http://www.math.dartmouth.edu/~euler/tour/tour_17.html
17. All Publications:
This list is accessible from the Eneström Index page (number 14 on the tour). Here is a complete list of the works of Euler, as numbered by Eneström. Once again, the titles can be viewed in their original languages, or in translation. Clicking on any Eneström number will bring up the corresponding E-page.
Enestrom Numbers 001-866: Original Titles | English Titles
...
(E?)(L?) http://www.heise.de/newsticker/e-i-pi-1-0-zum-300-Geburtstag-von-Leonhard-Euler--/meldung/88249
(E?)(L?) http://de.wikipedia.org/wiki/Eulersche_Identit%C3%A4t
(E?)(L?) http://de.wikipedia.org/wiki/Leonhard_Euler
...
Euler war extrem produktiv: Insgesamt gibt es 866 Publikationen von ihm. Ein grosser Teil der heutigen mathematischen Symbolik geht auf Euler zurück (z. B. "e", "p", "i", "Summenzeichen", "f(x)" als Darstellung für eine Funktion).
...
Nach Euler Benanntes
- Euler-Bernoulli-Gleichung, Differentialgleichung vierter Ordnung, die der Kontinuumsmechanik des Balkens zugrunde liegt
- Euler-Charakteristik, in der Topologie eine Kennzahl für geschlossene Flächen
- Eulersche Differentialgleichung, lineare gewöhnliche Differentialgleichung beliebiger Ordnung
- Euler-Eytelwein-Formel, Formel für Seilhaftung
- Satz von Euler-Fermat (Zahlentheorie)
- Eulersche Formel (Flächenkrümmung)
- Eulersche Formeln (harmonische Analyse)
- Eulersche Gerade: die Verbindungsgerade von Schwerpunkt, Höhenschnittpunkt und Umkreismittelpunkt eines Dreiecks
- Satz von Euler (Geometrie)
- Euler-Gleichungen (Eulersche Bewegungsgleichungen), Grundgleichungen der Hydrodynamik idealer (reibungsfreier) Flüssigkeiten (Strömungsmechanik)
- Eulersche Gleichungen (Kreiseltheorie), Eulersche Kreiselgleichungen
- Euler-Hierholzer-Satz
- Eulersche Identität, ein Spezialfall der Eulerschen Relation: eip + 1 = 0. (auch Eulersche Relation: exp(iz) = cos(z) + isin(z))
- Eulersches Integral erster und zweiter Gattung
- Eulersche Konstante siehe Euler-Mascheroni-Konstante (nicht zu verwechseln mit der Eulerschen Zahl).
- Euler-Lagrange-Gleichung
- Eulersche Last in der Balkentheorie die minimale axiale Last, die nötig ist, um eine Verbiegung zu bewirken
- Eulersche Linie (auch „Eulertour“ oder „Eulerkreis“) in der Graphentheorie: ein Kantenzug, der jede Kante eines Graphen enthält
- Euler-Maclaurin-Formel
- Euler-Mascheroni-Konstante ? = 0.5772...
- Euler-Maruyama-Verfahren zur Lösung von stochastischen Differentialgleichungen
- Eulersche f-Funktion in der Zahlentheorie: f(m) = Anzahl der zu m teilerfremden ganzen Zahlen a mit 0 < a < m
- Eulerscher Polyedersatz
- Eulersches Polygonzugverfahren (Integrationsverfahren für Differenzialgleichungen)
- Euler-Produkt, siehe Dirichletreihe
- Eulersche Turbinengleichung als Grundlage für die Kraftmaschine der modernen Stromerzeugung
- Eulersche Vermutung, Vermutung der Zahlentheorie und Verallgemeinerung der Fermatsche Vermutung
- die Euler-Wiege, eine kardanische Aufhängung, die in allen drei Eulerschen Winkeln drehbar ist
- Eulersche Winkel
- Weiterhin sind zu seinen Ehren ein Mondkrater (der Krater Euler) und der Asteroid (2002) Euler benannt. Auch ein Programm für numerische und symbolische Berechnungen trägt seinen Namen.
"§"
Eulersche Zahl (W3)
Im heutigen Sprachgebrauch ist Euler vor allem wegen der ihm zu Ehren so benannten "Eulerschen Zahl" "e" bekannt.
Euler hat die Zahl keineswegs entdeckt, auch war er nicht der Einzige, der ihre Bedeutung erkannt hat. Sicher ist, dass die Bezeichnung "e" auf "Euler" zurückgeht wie auch das "i" für die "imaginäre Einheit" und das griechische "S" ("Sigma", Σ) für die Bezeichnung einer "Summe".
Als Grund für die Wahl von "e" für die "Eulersche Zahl" ist (vermutlich) der Bezug auf die "Exponentialfunktion". Wer Euler aber wann die Ehre erwiesen hat, ihm mit der Benennung von "e" als "Eulersche Zahl" ein mathematisches Denkmal zu errichten, das haben die MathematikhistorikerInnen bislang noch nicht geklärt.
Die "Eulersche Zahl" ist definiert als die Summe (k=0 bis unendlich) von 1/k!. Dies ergibt eine irrationale Zahl die mit 2,7182 beginnt.
Wenn ein Kapital K(0) zu einem Zins von hundert Prozent angelegt und der Zins kontinuierlich verrechnet wird, dann erhält man am Ende eines Jahres ein Kapital K(1) = K(0) * e (statt K(0) * 2 wie bei einer jährlichen Verzinsung). "e" ist gleich dem Grenzwert von (1 + 1/n)^n, wenn n gegen unendlich geht.
Die "e-Funktion" ist die einzige Funktion, die mit ihrer Ableitung übereinstimmt.
Und das ist der Grund, weshalb das "e" bei fast jedem physikalischen Problem vorkommt: "e-Funktionen" bilden Grundlösungen für die mathematische Beschreibung aller möglichen natürlichen Vorgänge. Alles, was irgendwie schwingt, sich aufschaukelt oder sonstwie auf sich selbst zurückwirkt, ist ein Fall für e hoch x.
"e" findet man auch in einem Ausdruck, der die sogenannte Primzahldichte beschreibt (die Anzahl Primzahlen in einem bestimmten Intervall). Je mehr Zahlen man betrachtet, desto seltener tauchen Primzahlen auf. Exakt hergeleitet hat diesen Grenzwert noch niemand, doch scheint ihre Dichte im Unendlichen auf einen strikten Grenzwert zuzustreben. Dass in diesem Wert auch die Zahl "e" steckt, ist erstaunlich denn Primzahlen gehören ja eigentlich dem ganzzahligen Reich an.
Euler hat mit der Zahl "e" auch die wohl schönste mathematische Gleichung aufgestellt: e^(i*π) + 1 = 0. Man braucht gar nicht ausführlich auf die praktische Bedeutung der Gleichung einzugehen (die tatsächlich der Differentialrechnung den komplexen Raum und damit eine Unmenge neuer Anwendungen eröffnet hat), um eine Ahnung zu bekommen von der Begeisterung der MathematikerInnen für diese Formel. Sie verbindet auf einfachste Art die fünf wichtigsten Konstanten der Mathematik (die drei Einheiten 0, 1 und i [die Wurzel aus -1], dazu pi und e), ebenso wie die drei wichtigsten mathematischen Operationen: die Addition, die Multiplikation und die Potenz. Und alles das fügt sie mit einem einfachen Gleichheitszeichen zusammen.
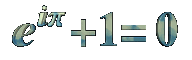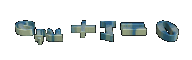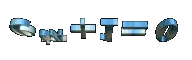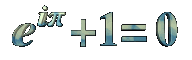
(E?)(L?) http://www.stmwfk.bayern.de/downloads/aviso/2003_1_aviso_38-47.pdf
...
Die Top Ten der schonsten mathematischen Satze:
1. e^iπ + 1 = 0
Ein Spezialfall der Eulerschen Formel (nach Leonhard Euler, 1707-1783), der die wohl wichtigsten Konstanten der Analysis in einen Zusammenhang bringt: die Eulersche Zahl e = 2,718282, die Kreiszahl π = 3,141593, die imaginare Einheit i = "Wurzel aus -1" sowie 0 und 1.
(E?)(L?) http://www.math.dartmouth.edu/~euler/
The works of Leonhard Euler online
The Euler Archive is an online resource for Leonhard Euler's original works and modern Euler scholarship. This dynamic library and database provides access to original publications, and references to available translations and current research.
The Archive is built around "E-pages." There is one of these pages for each of work written by Leonhard Euler (all 866 of them!).
Each page includes:
- The title of the work (and an English translation of the title)
- A summary of the work
- A description of where the work was originally published
- A description of where the work is published in the Opera Omnia
- A scanned pdf version of Euler's original publication
- A brief list of modern research papers which discuss or cite the work
"Original Documents (832)" findet man unter "What's Available ".
(E?)(L?) http://homepages.fh-giessen.de/~hg8070/ehm0607/sk29.pdf
1 + e^iπ = 0
(Diese Gleichung ist ein heißer Anwärter auf den Titel der schönsten Gleichung der Mathematik; es treten genau die wichtigsten Zahlen und die wichtigsten Operationen auf und sonst nichts.)
(E?)(L?) http://www.matheboard.de/mathe-tipp-zeigen,Mathematische_Zeichen.htm
(E?)(L?) http://www.mathe-online.at/mathint/lexikon/e.html
(E?)(L1) http://www.mathe-online.at/galerie.html
Zur Definition der Eulerschen Zahl e
(E?)(L1) http://www.schuelerlexikon.de/
(E?)(L?) http://de.wikipedia.org/wiki/Leonhard_Euler
Eulersche Zahl e = exp(1) = 2,71828...
Eulersche Zahlen verwandt mit den Bernoullischen Zahlen, treten als Taylor-Koeffizienten von sec(x) auf
(E?)(L?) http://de.wikipedia.org/wiki/Eulersche_Zahl
Dieser Artikel beschäftigt sich mit der Basis des natürlichen Logarithmus. Andere nach Euler benannte Zahlen und Zahlenfolgen sind unter Eulersche Zahlen (Begriffsklärung) aufgeführt.
Die eulersche Zahl e = 2,718281828459045235... (nach dem Schweizer Mathematiker Leonhard Euler) ist eine irrationale und sogar transzendente reelle Zahl.
Sie ist die Basis des natürlichen Logarithmus und der (natürlichen) Exponentialfunktion, die aufgrund dieser Beziehung zur Zahl e häufig kurz e-Funktion genannt wird. In der Infinitesimalrechnung (Differential- und Integralrechnung) spielt sie eine wichtige Rolle.
Inhaltsverzeichnis
- 1 Definition
- 2 Eigenschaften
- 3 Herkunft des Symbols e
- 4 Weitere Darstellungen für die eulersche Zahl
- 5 Anschauliche Interpretationen der eulerschen Zahl
- 5.1 Zinseszinsrechnung
- 5.2 Wahrscheinlichkeitsrechnung
- 6 Sonstiges
- 6.1 Weitere Eigenschaften
- 6.2 Entwicklung der Nachkommastellen von e
- 6.3 Die ersten 200 Nachkommastellen von e
- 7 Weblinks
- 8 Einzelnachweise
...
(E?)(L?) http://de.wikipedia.org/wiki/Eulersche_Zahlen
Die eulerschen Zahlen oder Euler-Zahlen (nach Leonhard Euler) sind eine Folge E(n) ganzer Zahlen, die durch die Taylorentwicklung der Hyperbelfunktion Secans hyperbolicus definiert sind.
...
(E1)(L1) http://ngrams.googlelabs.com/graph?corpus=8&content=Eulersche Zahl
Abfrage im Google-Corpus mit 15Mio. eingescannter Bücher von 1500 bis heute.
Dt. "Eulersche Zahl" taucht in der Literatur um das Jahr 1950 auf.
Erstellt: 2011-11
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z